In September 2024, the Commerce Department did something unprecedented: it imposed the first-ever worldwide export controls on quantum computing technology.
Not just quantum computers themselves. The entire supply chain—dilution refrigerators that cool qubits to near-absolute zero, cryogenic control systems, parametric amplifiers, even the specialized software used to calibrate these machines—all now require export licenses.
Any entity, anywhere, exporting these items to most destinations needs U.S. government approval.
Presumption of denial for adversaries.
The rule went further. It mandated reporting requirements for foreign nationals from sensitive countries working on quantum projects inside the United States.
Companies must now track and disclose what quantum technology they share with Chinese, Russian, or Iranian researchers on American soil.

Thirty-eight countries coordinated the rollout. The UK, EU members, Japan, Canada—all implemented equivalent controls even earlier or soon after. This wasn’t one nation acting unilaterally. It was the formation of a technology export cartel around quantum.
That level of international alignment doesn’t happen for speculative research. It happens when a capability crosses from interesting to foundational—when control over the technology translates to strategic leverage at the nation-state level.
China got the message. Beyond its estimated $15 billion commitment to quantum technologies, Beijing announced in March 2025 a national venture capital fund mobilizing $138 billion into AI, quantum, and hydrogen energy—signaling quantum as a foundational capability.
Meanwhile, the EU’s multi-billion-euro Quantum Flagship program continues advancing regional capacity. President Trump’s second administration has also elevated quantum to explicit strategic priority—naming it alongside AI and nuclear as focus technologies.
None of this is R&D theater. Yet the consensus view still treats quantum as speculative, a decade away, trapped in the lab.
That view is about three years out of date.
We’re no longer talking about whether quantum works. We’re talking about who controls the infrastructure when it scales—and which applications cross the commercial threshold first.
This primer exists because that threshold is closer than the market assumes.
How Quantum Computers Work
You’ve heard the talking points. “Exponentially faster.” “Qubits instead of bits.” “Game-changer for cryptography.”
All true. All useless for understanding what’s actually happening.
Here’s what you need to know.
Qubits Don’t Choose
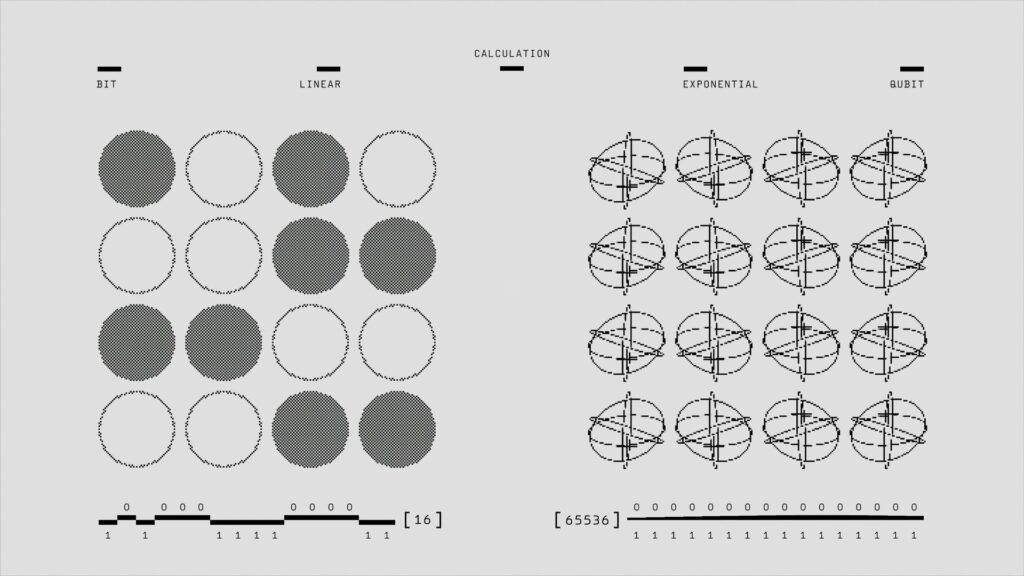
Classical computers process information as binary states: a transistor is either on (1) or off (0). Every operation—every search query, every AI inference, every transaction—is ultimately billions of these switches flipping in sequence. Fast, yes. But fundamentally serial in how they explore solution spaces.
Quantum computers exploit a different physics entirely.
A qubit—the fundamental unit of quantum information—exists in superposition. Unlike a classical bit locked to either 1 or 0, a qubit occupies both states until measured. It’s suspended in a probabilistic distribution defined by quantum mechanics.
Qubit Parallelism Leads to Exponential “Speedups”
However, the real unlock isn’t superposition itself. It’s what happens when you chain superposed states together across multiple qubits: quantum parallelism.
Qubits can be linked together through another quantum mechanical property called entanglement. When two qubits are entangled, measuring one instantly determines the state of the other, regardless of distance. Einstein called it “spooky action.”
Why does this matter?
A classical computer with 8 bits can represent one number at a time—say, 01101011. To evaluate a function across all 256 possible 8-bit numbers, it runs 256 sequential operations. Scale that to 300 bits, and you’re looking at more computational states than there are atoms in the observable universe. The problem becomes physically unsolvable within any reasonable timeframe.
A quantum computer with 8 qubits entangled in superposition represents all 256 states simultaneously. Apply a quantum gate—the equivalent of a logical operation—and you’ve just computed the function across the entire solution space in a single step.
In other words, quantum computers aren’t “faster” in the traditional sense. A classical computer escaping a maze tries path A, then path B, then path C.
A quantum system doesn’t walk those paths faster. Instead, it suspends all possible routes at once in superposition. Then, when you measure the system, it collapses to the optimal answer—if you’ve designed the quantum algorithm correctly.
This is an important distinction, because quantum computers won’t replace your laptop—they’re not general-purpose machines.
They’re precision instruments for specific problem classes where the solution space explodes combinatorially. Drug discovery. Materials simulation. Optimization across massive state spaces. That’s the investable domain.
Qubit Counts Are An Incomplete Picture
Here’s where a lot of quantum coverage goes wrong.
Mainstream outlets breathlessly report qubit counts—433 qubits, 1,000 qubits, 5,000 qubits—as if it’s a numerical race to some arbitrary finish line.
That’s not the full picture.
A quantum computer with 1,000 noisy qubits that decohere in microseconds is a physics demonstration, not a computational tool. What matters is coherence time and error rates—and those don’t scale with press release headlines.
Maintaining quantum states requires isolating qubits from any environmental interference—vibrations, electromagnetic fields, thermal noise. Superconducting qubits—the most mature architecture—operate at 15 millikelvin, colder than deep space, inside dilution refrigerators the size of chandeliers.

A single stray photon collapses superposition. This is called decoherence, and it’s a major engineering constraint. Coherence times—how long qubits maintain their quantum state—determine how many operations you can perform before the system degrades.
The second constraint is error rates. Quantum gates (the operations that manipulate qubits) are noisy. Most commercially relevant algorithms require millions of gate operations chained together. The math is unforgiving; errors compound exponentially.
Error correction solves this by encoding a single ‘logical’ qubit across multiple physical qubits, using redundancy to detect and fix errors in real time. But the overhead is severe: depending on the architecture, protecting one logical qubit can require anywhere from dozens to thousands of physical qubits.
These constraints explain why quantum has been ‘five years away’ for two decades. But coherence times have improved by orders of magnitude since 2020, and error rates have crossed critical thresholds.
We’re beginning to see real, if narrow, quantum advantage in commercial domains.
Application Domains: Where Value Forms First
Not every hard problem is a quantum problem. Quantum computers specifically excel at a narrow set of problem classes—they just happen to be extremely valuable.
Molecular Simulation: Solving Nature’s Puzzle
Every approved drug costs the pharmaceutical industry $2.6 billion. Most of that money—roughly 70%—pays for failure. Specifically, late-stage clinical trial failures: compounds that passed every computer model and every petri dish test, then collapsed the moment they encountered actual human biochemistry.
The bottleneck has been predictive accuracy.
Classical computers can’t actually simulate molecular behavior—they approximate it. For small, well-characterized molecules, those approximations work fine.
But drug discovery doesn’t happen in that zone. It happens at the computational edge: a 300-amino-acid protein binding to a novel small molecule, in search of a breakthrough cancer therapeutic.
This is why the industry still runs on wet-lab brute force. Synthesize 10,000 candidates. Screen them empirically. Keep the handful that show promise. Repeat. The entire pharmaceutical sector spends $300 billion annually on R&D, trying to buy its way around a computational ceiling.

In June 2025, a collaboration between IonQ, AstraZeneca, AWS, and NVIDIA demonstrated the disruptive potential of quantum computing in this domain. Their quantum-accelerated workflow achieved a 20-fold speedup simulating the Suzuki-Miyaura reaction.
If that name doesn’t mean much to you, here’s what matters—it’s a cornerstone chemical transformation in small-molecule drug synthesis. Not a toy problem. Not an academic exercise. A reaction class that underpins actual pharmaceutical production pipelines.
The hybrid system—IonQ’s 36-qubit Forte processor integrated with NVIDIA’s CUDA-Q platform on AWS infrastructure—compressed months of expected runtime into days while maintaining accuracy.
Drug discovery fuels a $2 trillion global pharmaceutical market. Pharma companies spend a decade bringing a single drug to market. With quantum computing, for the first time, we’re no longer just making slightly better guesses.
Materials science follows the same logic. Designing better catalysts for industrial processes, optimizing battery chemistries, engineering semiconductors with specific electronic properties—all of these require understanding atomic-scale interactions that classical systems struggle to model.
Optimization: When Milliseconds Cost Millions
The second high-value domain is combinatorial optimization—problems where you’re searching for the best solution across an astronomically large solution space.
Think: routing 10,000 delivery trucks across a metro area with shifting traffic, weather, and demand. Or optimizing a supply chain with seven million variables. Or portfolio construction across 8,000 securities with complex covariance structures.
Classical optimization algorithms use heuristics—educated guesses that get you close to optimal. They work, but they leave value on the table. Quantum algorithms like QAOA (Quantum Approximate Optimization Algorithm) explore the entire solution space in superposition, collapsing to near-optimal solutions faster than classical methods.
Logistics is the obvious target. UPS saves $300-400 million annually from its route optimization efforts—quantum systems that improve efficiency by even 5-10% justify deployment costs.
Finance is positioning aggressively. JPMorgan, Goldman Sachs, and Citigroup all have quantum teams exploring portfolio optimization, risk modeling, and derivative pricing. The edge in high-frequency trading or credit default swap valuation doesn’t need to be large in an industry that measures gains in pips.
Cryptography: The Double-Edged Sword
This is the application that gets the most press and the least clarity.
Quantum computers threaten current cryptographic standards because of Shor’s algorithm—a quantum algorithm that can factor large numbers exponentially faster than any known classical method. RSA encryption, which secures most internet traffic, relies on the assumption that factoring is computationally infeasible. A fault-tolerant quantum computer breaks that assumption.
Previously, breaking RSA-2048 encryption was estimated to require 20 million physical qubits. But in May 2025, Google Quantum AI published new estimates: one million noisy qubits running for under a week—a bar 95% lower than what it was six years prior. The drop came from algorithmic improvements, not just hardware advances.
No current quantum system has the performance specs needed. But the threat is real enough that NIST has already published post-quantum cryptographic standards, and federal agencies are under directive to migrate by 2035.
Harvest Now, Decrypt Later (HNDL)
More concerning: adversaries aren’t waiting for Q-Day to act. They’re already executing what’s known as “Harvest Now, Decrypt Later” (HNDL) attacks—collecting encrypted data today with the intent to decrypt it once quantum systems mature.
The strategy is simple. Intercept communications or exfiltrate encrypted databases. Store them indefinitely. Wait.
The data doesn’t need to be decrypted immediately—it just needs to retain value over a decade or longer. Financial records. Healthcare data. Trade secrets. Diplomatic cables. Government classified information. Anything with a long sensitivity window becomes a target.
This shifts the threat model. Organizations evaluating quantum risk often ask: “When does Q-Day arrive?” Wrong question. The breach is happening now; the decryption happens later. By the time quantum systems reach the capability threshold, the data has already been collected.
The opportunity here isn’t the threat—it’s the countermeasure:
Post-quantum cryptography will be a mandated rollout across every bank, every hospital system, every government network, every enterprise handling sensitive data. Companies building quantum-resistant encryption, secure key distribution networks, or crypto-agile systems that can swap algorithms without full infrastructure overhauls will capture revenue in the near-term.
The Path to Commercial Quantum Computing
Quantum computing isn’t one technology—it’s at least five competing hardware architectures, each with different physics, different error profiles, and different paths to scale.
Understanding which approaches are maturing fastest matters because quantum hardware determines quantum software in ways classical computing never did. When Intel’s x86 architecture won the PC wars, developers could still write portable code—the instruction set abstracted away the underlying silicon.
Quantum doesn’t work that way. Algorithms written for superconducting qubits don’t port to trapped ions. Error correction strategies are architecture-specific. The first platform to reach fault tolerance doesn’t just win market share—it defines the development stack, locks in the talent pool, and forces everyone else to either integrate or settle with defensible niches.

Superconducting Qubits: The Incumbent Platform
Superconducting qubits are the most mature architecture. IBM, Google, and Rigetti have collectively deployed thousands of physical qubits across cloud-accessible systems. IBM’s roadmap targets 100,000+ qubits by 2033.
The qubits are patterned onto silicon wafers using lithography, thin-film deposition, and etching—techniques borrowed from semiconductor manufacturing. This gives superconducting systems a significant fabrication advantage over approaches that rely on trapping individual atoms or routing single photons.
That said, superconducting qubits do require exotic materials, along with “Josephson junctions” that have no analog in conventional transistors. That means they can’t directly leverage existing chip fabs; they still require purpose-built facilities.
The constraint is coherence. Superconducting qubits decohere in microseconds to milliseconds. That limits circuit depth before errors overwhelm computation. Error correction solves this by encoding one logical qubit across multiple physical qubits—but the overhead is severe. Ratios can reach 1,000 physical qubits per logical qubit.
Superconducting systems will likely dominate the next five years of commercial deployments, particularly for optimization and early-stage molecular simulation. Whether they scale to fault-tolerant cryptographic applications remains an open question.
Trapped Ion Qubits: Precision Over Scale
Trapped ion systems maximize qubit quality rather than qubit count.
IonQ, Quantinuum, and eleQtron suspend individual ions in electromagnetic fields, then manipulate them with lasers. Each ion is naturally identical—no fabrication variability. Coherence times measure in seconds rather than microseconds. Gate fidelities exceed 99.9%.
This translates to dramatically lower error correction overhead. Where superconducting systems need 1,000 physical qubits per logical qubit, trapped ion architectures could hit the same thresholds with ratios closer to 10:1 or 100:1.
The constraint is scale. Trapped ion systems connect qubits by shuttling ions between zones or using photonic links. Both introduce latency and complexity. Current systems top out at dozens of qubits; reaching thousands requires solving interconnect challenges that don’t yet have clear solutions.
Trapped ions are precision instruments. For applications that tolerate smaller qubit counts but demand high fidelity—drug simulation, certain cryptographic workloads—this architecture has a near-term edge.
Silicon Spin Qubits: CMOS-Native Quantum
Silicon spin qubits encode information in electron spin states trapped in silicon—the same base material that powers conventional chips.
The defining advantage: full CMOS compatibility.
Unlike superconducting systems that still need purpose-built facilities, silicon spin qubits can be fabricated in existing semiconductor fabs using standard processes. Intel is manufacturing them in its production lines. Diraq recently demonstrated 99% fidelity spin qubits on 300mm wafers—the industry-standard format for every smartphone processor and data center chip.
Silicon spin qubits also operate warmer—1-4 Kelvin versus millikelvin for superconducting systems. They’re orders of magnitude smaller, enabling higher densities.
The remaining constraint is control at scale. Diraq demonstrated precision with individual devices, but replicating this across thousands of qubits with the uniformity needed for fault-tolerant systems remains unproven. Gate operations are also slower than superconducting approaches.
Silicon spin is a longer-timeline bet. But if the control problem gets solved, this architecture inherits the scalability and cost structure of the entire semiconductor industry: advanced foundries, established supply chains, mature process control, economies of scale.
Neutral Atoms: Density Dark Horse
Neutral atom systems trap arrays of atoms in optical tweezers, then manipulate them with lasers.
The scaling advantage: you can pack neutral atoms far more densely than superconducting circuits or trapped ions. QuEra demonstrated 256-qubit systems in 2023 and targets 10,000+ qubits by 2026. The architecture also enables mid-circuit measurement and qubit reuse—reducing error correction overhead by allowing qubits to reset and redeploy during computation.
The risk is technical maturity. Gate fidelities lag superconducting and trapped ion systems. Coherence times remain a constraint. Neutral atoms might leapfrog incumbents on scale and cost—or hit fundamental physics limits before reaching commercial relevance.
Photonic and Topological: Long-Term Moonshots
Photonic quantum computers use light particles as qubits, operating at room temperature with inherently low error rates. If the architecture scales, it solves refrigeration and potentially error correction simultaneously.
The catch: photonic systems require fault-tolerant designs from day one. You can’t build a “noisy intermediate-scale” photonic computer—it either works fault-tolerantly or not at all. PsiQuantum is betting nearly $1 billion that they can fabricate million-qubit photonic systems using modified semiconductor foundries. If it works, it’s transformative. If it doesn’t, there’s no salvageable milestone.
Topological qubits promise intrinsic error resistance by encoding information in quantum states naturally protected from decoherence. Microsoft has pursued this for a decade without demonstrating a working topological qubit at scale. It remains the highest-risk bet in the sector.
The Fault-Tolerance Threshold
All of these architectures converge on one question: when do we cross from noisy systems to fault-tolerant quantum computers capable of running million-gate algorithms reliably?
Consensus timelines have compressed. In 2020, fault tolerance was projected for 2035-2040. Today, leading players target 2028-2030. IBM aims for fault-tolerant systems by 2029. Quantinuum and IonQ both claim pathways to commercially relevant logical qubits within three years.
The inflection happens when error-corrected logical qubits become cheaper and more reliable than noisy physical qubits. Once that threshold is crossed, applications requiring fault tolerance—cryptography, large-scale molecular simulation, complex optimization—unlock rapidly.
We’re not there yet. But the trajectory is clear, the capital is committed, and the engineering is derisking.
Reading the Quantum Signal
For investors, the trickiest part isn’t understanding quantum mechanics. It’s filtering quantum news.
Every qubit count milestone generates headlines. Every corporate partnership gets a press release. Every “quantum-inspired” algorithm claims a breakthrough. Most of it is positioning, not progress.
Here’s what actually matters:
- Logical qubit demonstrations. Physical qubit counts are physics demos. Logical qubits—error-corrected, stable, usable for real computation—are the derisking milestone. When companies report logical qubit milestones, that’s signal.
- Enterprise pilots moving to production. Pharma companies, financial institutions, and logistics operators are already running quantum experiments. Most are exploratory. Watch for the transition from “proof of concept” to “deployed workload” on real operations budgets.
- Algorithmic compression. Hardware timelines matter, but algorithmic breakthroughs act as a force multiplier. Google’s recent estimate dropping cryptographic threat requirements from 20 million qubits to 1 million came from better algorithms.
- Government procurement and defense contracts. When defense agencies move from R&D grants to acquisition contracts, the technology has crossed a maturity threshold. Quantum sensing is already there. Quantum computing is approaching it.
We’ll continue tracking these vectors as quantum matures. The geopolitical stakes are already clear—export controls, strategic funding, supply chain positioning. The technical trajectory is compressing. Commercial applications are en route.